1074. Number of Submatrices That Sum to Target

LeetCode 1074. Number of Submatrices That Sum to Target

Description

Given a matrix and a target, return the number of non-empty submatrices that sum to target.

A submatrix x1, y1, x2, y2 is the set of all cells matrix[x][y] with x1 <= x <= x2 and y1 <= y <= y2.

Two submatrices (x1, y1, x2, y2) and (x1', y1', x2', y2') are different if they have some coordinate that is different: for example, if x1 != x1'.

Example 1:

Input: matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
Output: 4
Explanation: The four 1x1 submatrices that only contain 0.

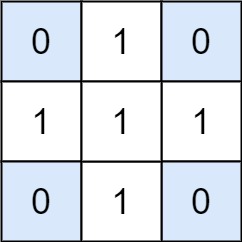
Example 2:

Input: matrix = [[1,-1],[-1,1]], target = 0
Output: 5
Explanation: The two 1x2 submatrices, plus the two 2x1 submatrices, plus the 2x2 submatrix.

Constraints:

• 1 <= matrix.length <= 100

• 1 <= matrix[0].length <= 100

• -1000 <= matrix[i] <= 1000

• -10^8 <= target <= 10^8

Tags

Array, Dynamic Programming, Sliding Window

Solution

From LeetCode 560. Subarray Sum Equals K we know how to obtain the subarrays whose sum equal to a certain target value. This problem extends it to 2D scenario, but we can also take advantage of the solution of 1D version subarraySum(). We traverse all continuous rows permutations, and sum up these rows along each columns to obtain a 1D array. This array and target are the arguments of subarraySum(). The final result is the sum of all return values of this function.

Complexity

• Time complexity: $O(m^2\times n)$

• Space complexity: $O(n)$

Code

func numSubmatrixSumTarget(matrix [][]int, target int) int {
	var ans int
	for i := range matrix { // upper bound
		colSum := make([]int, len(matrix[0])) // columns sum
		for _, row := range matrix[i:] {      // lower bound
			for j, v := range row {
				colSum[j] += v
			}
			ans += subarraySum(colSum, target)
		}
	}
	return ans
}

func subarraySum(nums []int, k int) int {
	ans, preSum, m := 0, 0, map[int]int{0: 1}
	for _, num := range nums {
		preSum += num
		ans += m[preSum-k]
		m[preSum]++
	}
	return ans
}

Reference

1. 元素和为目标值的子矩阵数量