897. Increasing Order Search Tree

LeetCode 897. Increasing Order Search Tree

Description

Given the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.

Example 1:

Input: root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]

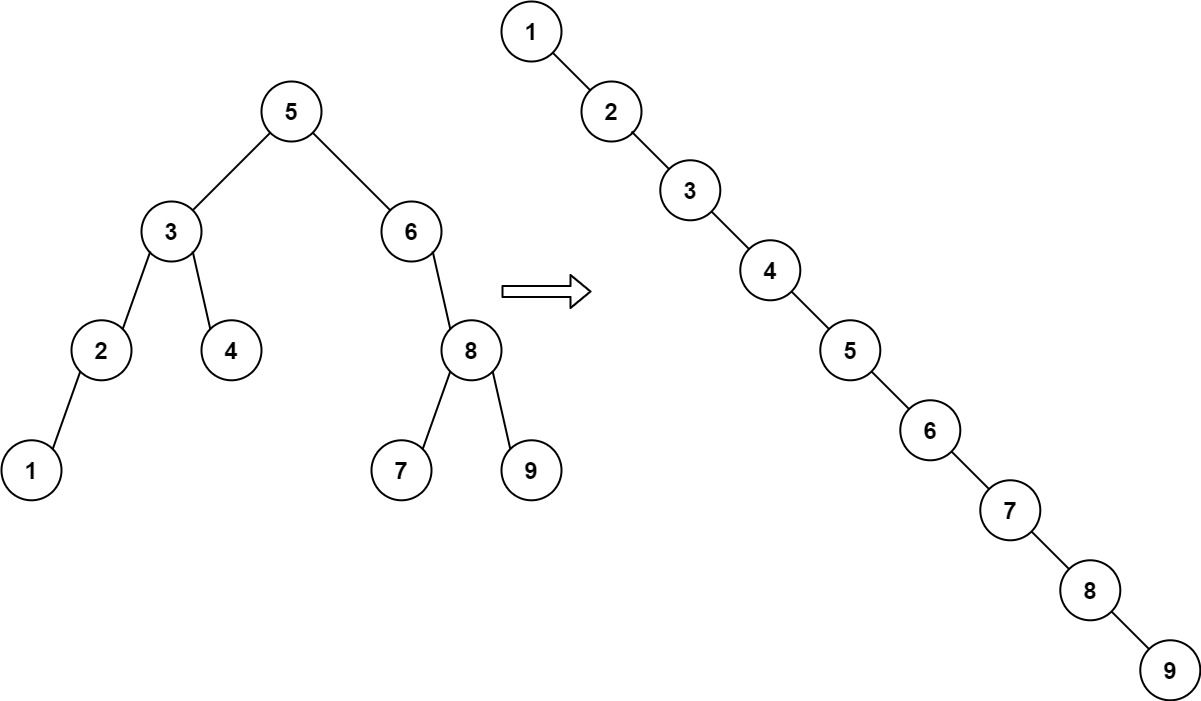
Constraints:

• The number of nodes in the given tree will be in the range [1, 100].

• 0 <= Node.val <= 1000

Tags

Tree, Depth-first Search, Recursion

Solution

We initialize a dummy root node to store the output tree. We perform the in-order traverse on the input tree. For each visited node, we create a new node with the same value and assign it to the right-child of the rightmost node of the output tree. Finally, we return the right-child of the dummy root.

Complexity

• Time complexity: $O(n)$

• Space complexity: $O(n)$

Code

func increasingBST(root *TreeNode) *TreeNode {
	dummy := &TreeNode{}
	ans := dummy
	var stack []*TreeNode
	for len(stack) > 0 || root != nil {
		for root != nil {
			stack = append(stack, root)
			root = root.Left
		}
		root = stack[len(stack)-1]
		stack = stack[:len(stack)-1]
		dummy.Right = &TreeNode{Val: root.Val}
		root, dummy = root.Right, dummy.Right
	}
	return ans.Right
}