331. Verify Preorder Serialization of a Binary Tree

LeetCode 331. Verify Preorder Serialization of a Binary Tree

Description

One way to serialize a binary tree is to use preorder traversal. When we encounter a non-null node, we record the node's value. If it is a null node, we record using a sentinel value such as '#'.

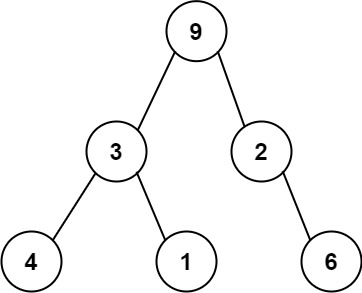
For example, the above binary tree can be serialized to the string "9,3,4,#,#,1,#,#,2,#,6,#,#", where '#' represents a null node.

Given a string of comma-separated values preorder, return true if it is a correct preorder traversal serialization of a binary tree.

It is guaranteed that each comma-separated value in the string must be either an integer or a character '#' representing null pointer.

You may assume that the input format is always valid.

• For example, it could never contain two consecutive commas, such as "1,,3".

Example 1:

Input: preorder = "9,3,4,#,#,1,#,#,2,#,6,#,#"
Output: true

Example 2:

Input: preorder = "1,#"
Output: false

Constraints:

• 1 <= preorder.length <= 104

• preoder consist of integers in the range [0, 100] and '#' separated by commas ','.

Follow up: Find an algorithm without reconstructing the tree.

Tags

Stack, Tree

Solution

It is always true for a Tree or a Directed Graph that the sum of in-degree of all nodes is equal to the sum of out-degree of all nodes. There are 3 types of nodes:

• Root: in-degree = 0, out-degree = 2;

• Non-leaf (expect the root): in-degree = 1, out-degree = 2;

• Leaf: in-degree = 1, out-degree = 0;

Based on these facts, we can initialize a variable degree = 1 and iterate over the splitted input. In the loop, we decrease degree by 1 which is the in-degree (this is also why we initialize degree with 1 since the root has no in-degree). At this time, if degree < 0 we can early return false, because it should not be a negative value since we have not visited its children yet. Then, degree += 2 if it is a non-leaf node, a.k.a. "#". At last, we return degree == 0 to validate if it is a legal tree.

Complexity

• Time complexity: $O(n)$

• Space complexity: $O(1)$

Code

func isValidSerialization(preorder string) bool {
	nodes, degree := strings.Split(preorder, ","), 1 // degree is init with 1 since root has no in-degree
	for _, node := range nodes {
		degree--
		if degree < 0 { // degree should not be non-pos number since we have not visited its children yet
			return false
		}
		if node != "#" {
			degree += 2
		}
	}
	return degree == 0
}

Reference

1. 拍案叫绝的两种解法：「栈」和「入度出度」